���_�F��ʉ�����
�O�X�^��2���A�h���t�ƃX�E�F�[�f���R
���F�I�I�^�i@masa0ta�j�A����i@Hatashirorz�j
1�D�ړI
�i�|���I���́A�������ȑO�Ɏ��l�̈̑�Ȏw�����������Ƃ��āA�Ñ�ȍ~�̕M���ɃO�X�^��2���A�h���t�̖��O���������Ɠ`���B�����Ĕނ������������R�����v�Ɣނ��������X�E�F�[�f���R�̊q�X���鏟���́A���j�ƃ}�C�P���E���o�[�c�����āA�R���v���Ƃ܂Ō��킵�߁A�O�X�^��2���A�h���t�́u�ߑ�R���̕��v�Ƃ��Č���Ɏ���܂ŗh�邪�ʖ������Ă���B
�������A�ŋ߂̌����́A�O�X�^���̌R�����v�̉e�����ĕ]������X���ɂ���B���ۂ̂Ƃ���A�ނ��n�n�����Ƃ���Ă����u���v�v�̐��X�́A�ˑR�ɐ��܂ꂽ���̂ł͂Ȃ��A����܂ł̌R���I���W�Ǝ��s����̕����̒��Ō����ׂ����̂ł���A���邢�͒P�Ȃ����ł����Ȃ����̂���������܂܂�Ă���[�P]�B
���������̌����́A�w�����O�X�^���Ƃ��̌R���̔\�͂�ے肷����̂ł͌����ĂȂ��B�������ɐ_�b�̎���͏I������B����ł��ނ炪�O�\�N�푈�̒��Ղɂ����āu�X�E�F�[�f�����v�ƌĂ���̎�������グ�����Ƃ͕�����Ȃ������ł��邩�炾�B
�{�e�ł͌R���I�y���[�V�����i�R��OR�j�̓��ł��A��K�͂ȌR�c�̉��͂����헝�_�̈�Ƃ��Ēm�����ʉ����胂�f���iQJM�FQuantified Judgement Model�j��p���āA1630�N��O���ɂ�����O�X�^��2���A�h���t�Ɣނ��b���グ���X�E�F�[�f���R�̔\�͂͂��A�萫�I�ȕ]���ɒ�ʉ����ꂽ�w�W��t�^����B
2�D���p�����j�f�[�^
�{�e���L�q�����ɂ����āA���̌����т̃f�[�^�͋ɂ߂ďd�v�ł���B�������ߐ��̐푈�ɂ����镺���⑹�Ղ̋L�^�͎�X�G���ł���A�M�����������Ă���B�O�\�N�푈�̊e���ɂ����Ă���O�ł͂Ȃ��B���̂��ߖ{���ł���A���͎Җ{�l���j�����ڍׂɌ������A�^�l���A���Ȃ��Ƃ����͎Җ{�l���m�M�ł���^�l�����肷��K�v������B�����A�����̎d���͕M�҂̎�ɗ]����̂ł���A�����ł͊��ɐ����������Ă���ȉ��̌������ʂ�p���Đ��l�f�[�^�Ƃ��邱�ƂƂ����B
1. Guthrie, William P. Battle of the Thirty Years War From White Mountain to Nordlingen, 1618-1635. London: Greenwood Press, 2002.
2. Guthrie, William P. The Later Thirty Years War: From the Battle of Wittstock to the Treaty of Westphalia. London: Greenwood Press, 2003.
3�D��ʉ����胂�f���iQJM�j�ɂ���
�@��ʉ����胂�f���i�ȉ��AQJM�j�̓A�����J���R�o�g�̃g�����@�[�EN�E�f���s���C�iTrevor N. Dupuy�j�ɂ����ꂽ��K�͂ȉ��̕��͂����Ƃ����헝�_�ł���B����͌�헝�_�Ƃ��Ĉ�ʂɒm���Ă��郉���`�F�X�^�[�E���f���ƈقȂ�N���E�[���B�b�c�̊T�O��莮�����邱�ƂŌ����ʉ��������f���ł���B
�萫�I�Ȋϑ����ʂ���b�Ƃ��Ă��邱�Ƃ���R��OR�̐��E�ł͕]�����Ⴂ�X���ɂ��邪�A���͂̑O������������`�F�X�^�[�E���f����1������2�����̒��ԂɈʒu���A�����������ߐ��̉��ɂ����ẮA�ł��K�ȗ��_�ł���ƍl����B�ȉ��ɂ��̊T�O��������[�Q]�B
P=S�~V�~Q
�iP�F���ΓI������́BS�F��́BV�F���v�f�W���B
Q�F�R�̎��A���ΓI�퓬����CEV�Ƃ��Ď������j
4�D���S�̌v�Z
�@QJM�ł̐�͌v�Z�ɂ́A����ȏ�̒P�ʂō\������鑽����̌R�̐퓬�\�͂��r����ۂɒ���Ă���Η͕]�_�ifirepower score�j�A�v���[�`�̊T�O���̗p����Ă���B����͍����^�����`�F�X�^�[�E���f����A�����J�R��TACWAR���ł��̗p����Ă���T�O�ŁA�e����̔\�͂��A�e���f���ɂ���߂�ꂽ��ɏ]�����l������l���ł���B
�ȉ��ɋߐ��ɂ�����S�̎��������B����͊e�X�̕�����͒l�iW�FWeapons Effectiveness�j�ɁA���̕���ɂ���Ċe�X�ɒ�߂��Ă���W��r���|�����l�̑��a�ɂ��Z�o�����B
S=Wi�~ri+Wc�~rc+Wg�~rg
�i�Y����i�F�����@�Y����c�F�R���@�Y����g�F�C���j
�����āA���̕�����͒lW�́A���_�v���w���iTLI: Theoretical Lethality Index�j�ƁA�^�p�v���w���iOLI�FOperational Lethality Index�j�A�����ĒP�ʕ��͂�����̐��������R�̕��U�v�f�iDi�FDispersion factor�j��p���āA�ȉ��̎��ŕ\�������[�R]�B
TLI=�ˌ����x�~�З͔͈��~�E�������~�˒��v���~���m���~�M����
OLI=TLI/Di
W=N�~OLI
Di�F100,000�����W�J����̂ɕK�v�Ȗʐρikm2�j�@�@N�F�����A�C��
���_�v���w��TLI��1�������[�g���ɓG���m1�������z����Ƃ������I�ȑz�艺�ɂ����镺��̔\�͒l�������A���̑傫�����l�����Ă��Ȃ����_�l�ł���B���̂��߁A�P�ʕ��͂�����̕��z������Di��p���ĉ^�p�v���w��OLI���Z�o���Ă���B
�@�{��͂ŗp�����O�\�N�푈�ɂ����钷���A�R���p�̌��A�}�X�P�b�g�e�A�Z�e�A��C�̗��_�v���w��TLI��\1�Ɏ����B
�\ 1�@���_�v���w��TLI[�S]
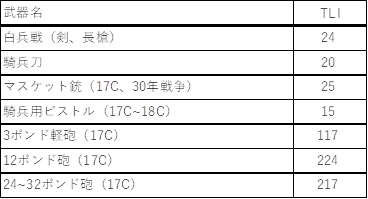
�����āADi�ɂ��Ă͉��n�}����T�Z�̕z�w�ʐς��Z�o���āA100,000���ł������ꍇ�̖ʐςɊ��Z�����B���̌��ʁA�{�e����舵�����ɂ����Ă�Di=2�`8���B�܂��A�f���s���C�͊e����̕��ϒl���Z�o���Ă���A�����\2�Ɏ����B������{�������n�}����̊e�T�Z�l�ƃf���s���C�ɂ��17���I�̕��ϒl�͊T�ˍ��v������̂ł������B
�\ 2�@���U�v�fDi[�T]
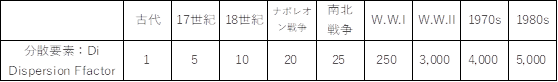
5�D���v�f�W��V�ɂ���
�@���v�f�W��V�͐��̕ϓ��v�f�ł���A�傫�������Ċ��v�f�A�l�I�v�f�A�^�p�v�f��3������B�f���s���C�������v�f�̈ꗗ��\3�Ɏ����B�����QJM��@�̍ł��d�v�ȓ��F�ł���A�n�`��V��A�G�߂Ƃ�����������₷���v�f�݂̂Ȃ炸�A�N���E�[���B�b�c���푈�𗝉������Ō����đa���ɂ��Ă͂Ȃ�Ȃ��Ƃ������_�I�v�f��u���̖��v�����f�������邽�߂ɓ������ꂽ�W���ł���B
�@���R�̂��ƂȂ���A�����̌W���͗��R�ɋ��ɓ������l�Ƃ͂Ȃ�Ȃ��B�Ⴆ�Βn�`�ł͎��ɓK�����n�`�́A�U�߂�ɂ͓���n�`�ƂȂ邩��ł���B�l�I�v�f�A�^�p�v�f�ɂ��Ă͗��������܂ł��Ȃ����낤�B�����̏ꍇ�A�����̌W����0.1�`2.0�̊Ԃ̐��l���p������[�U]�B
�\ 3�@���v�f�W��[�V]
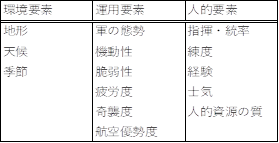
6�D���ΓI�퓬����CEV�̌v�Z
�@QJM�ɂ����āACEV�͌R�̎����퓬���ʂɗ^����e���������l�ł���A���_��̐��p�ɑ����ʂ̑傫���̔���������̂ł���BCEV�̎����ȉ��Ɏ����B�Y������A,B�͊e�R�iA�R�AB�R�j�������B
CEVA=(pB/pA)/(RB/RA)�@ CEVB=1/ CEVA
p=S�~V
R=MF+ESP+Ecas
p�F���_��́i���͂Ɛ��v�f�W���݂̂��l�������ꍇ�̐�́j
MF�F�C���B���x�i�C�����ǂꂾ���B�������̂��������l�B1�`10�̒l�����j
ESP�F�l���ʐό����i�l�������n��ʐς̔䗦�j
Ecas�F���Ռ����i�l�I���Ղ̔䗦�j
�@���̎��́A���_��͔�Ɛ�ʔ䂪�����ł����CEV��1.0�ƂȂ邱�Ƃ������Ă���A����͐�͔�Ɍ���������ʂ����������Ƃ��Ӗ�����B���̂���CEV<1.0�ƂȂ�Η��_��͔�Ɍ�����Ȃ���ʂ����������Ȃ������A�܂��͂ʂɗp���������̈����i���̈����j�킢���������Ƃ������B�t��CEV>1.0�͗��_��͔�ȏ�̐�ʂ����������Ƃ������̂ŁA��͂������悭�p�������̗ǂ��킢���������ƂɂȂ�B����CEV�͓G���������ꍇ�͋t���ƂȂ邪�A���ӂ��Ȃ���Ȃ�Ȃ��̂́A���Βl�ł��邩�王�_���Œ肵�Ăǂ��炩��CEV���|�������ΓI�������P���Z�o�����ꍇ�A���������CEV��1.0�Ƃ��Ĉ���˂Ȃ�Ȃ��Ƃ������Ƃł���B
�f���s���C�̒����ɏ]���ΐ�������̃h�C�c�R��W.W.I�ɂ�����CEV��1.0�`1.6�AW.W.II�ł�1.0�`1.5�ł���A�����̕���CEV��1.2���x�ƂȂ�[�W]�B����͑����̏ꍇ�h�C�c�R���A���ς��Đ��I�ł���Ȃ������͍����Ă������Ƃ̏؍��ł��낤�B
7�D�{�e�̍l�@�Ώ�
�@����l�@�̑ΏۂƂ����킢�́A�O�\�N�푈�X�E�F�[�f�����ƌĂ�鎞��ɂ����čs��ꂽ�܂̐킢�ƁA�t�����X�E�X�E�F�[�f�����̐킢��́A�v�Z�ł���B�ȉ��ɂ��̐킢������[�X]�B
1. ��ꎟ�u���C�e���t�F���g���i1631�N�j
2. ��ꎟ���q��̐킢�i1632�N�j
3. �A���e�E���F�X�e�̐킢�i1632�N�j
4. �����b�c�F�����i1632�N�j
5. �l���g�����Q�����i1634�N�j
6. ���B�b�g�X�g�b�N���i1636�N�j
�܂����̎���̔�r�ΏۂƂ��čŏ��Ƀi�|���I���푈�ɂ�����u�A�E�X�e�����b�c���i1805�N�j�v�����グ��B����̓f���s���C�����̐킢��QJM�ɂ��l�@�̑ΏۂƂ��ėp���Ă���A����̔�r�ɂ������ɂȂ�Ɣ��f�������߂ł���[�P�O]�B
8�D�A�E�X�e�����b�c���
�@�O�\�N�푈�̐�����舵���O�Ƀf���s���C�̌��ʂ���ɂ��A��r�Ώۂł���A�E�X�e�����b�c���ɂ��Ă�QJM�ɂ�镪�͂ƁA���̓��e�ɂ��Đ�������B
�@�܂�QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�1�Ɏ����B���̐킢�ɂ����ĕ��͗ɂ������t�����X�R�͑Ε��哯���R�i���V�A�E�I�[�X�g���A�A���R�j��ɂ��đ叟�������߂��B���̂��ߖ{�v�Z�ɂ����ĔC���B���xMF�̓t�����X�R��9�i�叟���j�A�����R��2�i�s�k�j�Ƃ��Ă���B�܂��A���v�f�W��V�Ƃ��āA�t�����X�R�ɂ͋@���v�f1.1��[�P�P]�A��P�v�f�Ƃ���1.6��t�^�����B����́A�t�����X�R�̋@���͂������R�ɑ��Ĕ�r�D���ɂ����������ƁA�v���c�F�����n�ւ̍U���������I�Ȋ�P�Ƃ��Ď�舵���ɂ����p�ł������Ƃ����]���������l�ł���B
�@���̌��ʁA���_���͔�SA/SB�ɂ�����0.86�ƕs���ɂ������t�����X�R�́A1.76�̐��v�f�W���āA���_��͔�pA/pB�ɂ����ċt�ɗD���̗���ɂȂ�B���͔䂨��ѐ�͔�̎������s�̖ڈ���\4�Ɏ����B�������A���̔䗦�ł����Ă����ۂ̐�ʂɌ������قǂł͂Ȃ������B��ʔ�RA/RB��3.69�ł���������ł���[�P�Q]�B
SA/SB=0.86 SB/SA=1.17
pA=SA�~VA=240,304 pB=SB�~VB=159,834
pA/pB=1.50 pB/ pA=0.67
RA/RB=3.69
CEVA=(pB/pA)/(RB/RA)= (RA/RB)/(pA/pB)=2.46
���㎮�ɂ�����A�R�̓t�����X�AB�R�͑哯���R�������B
�\ 4�@���͔�E��͔䏟�s�ڈ�
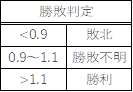
�@�܂�A���ɐ��v�f�W��V�𑝂��v�f���Ȃ�����A�����R�ɑ���t�����X�R�̑��ΓI�퓬����CEVA��2.46�ƂȂ�B�����Ńf���s���C�͑��ɗv�f�����݂��Ȃ������������B�f���s���C�����ڂ����̂́A���[�e�����[������̌o������E�F�����g�����q�ׂ��Ƃ����u���ɂ���i�|���I����4���̕��̉��l������v�Ƃ������t�ł���[�P�R]�B����������́A1815�N�̍Ő������߂��A�G���ނ̂������w��̃i�|���I����]�����Ă̌��t�ł������B�����Ńf���s���C�́A1815�N�ɂ����Ă���4���̉��l������Ƃ���Ȃ�A�S�����̃i�|���I���ƁA�i�|���I���̂������w��ł��Ȃ��G�Ƃ̊Ԃɂ͍X�ɑ傫�ȍ����������ł��낤�Ɛ��肵�āA���ɂ���i�|���I���̉��l��6���ƌ��ς������B
�@�������ăt�����X�R�̕����ƋR���ɂ��ꂼ��3���̕����𑫂��ƁA�A�E�X�e�����b�c���ɂ�����t�����X�R�̗��_���͂�1.6�ƂȂ�A�V���̗��_���͔�͖�1.9�ƂȂ����B����ăf���s���C�̓i�|���I���̎w���E�����v�fle��1.9�Ɛ��肵���B
�����ăi�|���I���̎w���E�����v�fle��1.9�Ƃ����ꍇ�A�����R�ɑ���t�����X�R��CEV��1.3�ƂȂ�B����͗���펞�ɂ����镽�ϓI�ȃh�C�c�R��CEV��1.2�ɋ߂����A�Ó��Ȓl�ł������B
��SA/SB=0.86���VSA/SB=1.6�@���i�VSA/SB)/�i��SA/SB�j��1.9
CEV�i�w���E�����v�f�l�������j=2.46��1.9�~1.3
2.46�~75%��1.9
�ȏ�̂��Ƃ���AQJM��p�����A�E�X�e�����b�c���̕��͌��ʂ́A�i�|���I���Ƒ嗤�R�̑g�ݍ��킹���A�G�ł��铯���R�Ɣ�r����Ƌ����قnj����悭��͂��^�p���Đ�ʂ����������ƁA�����āA�i�|���I���̎�r�̍v���x�����́A���Ȃ��Ƃ����̓��̂��悻�l���̎O�A�܂�75%�ɒB���邱�Ƃ�������[�P�S]�B
�ł́A�O�\�N�푈�ɂ�����O�X�^��2���A�h���t�ƃX�E�F�[�f���R�͂ǂ��ł������̂��낤���H�@
9�D��ꎟ�u���C�e���t�F���g���
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�2�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\5�Ɏ���[�P�T]�B�c��R�̑��Ղɂ��Ă͐퓬��̒nj���ōX��3,400�����lj������ꍇ��A�����Ƀ��C�v�c�B�q�ō~������3,000����������l�������邪�A�����ɂ��Ă͐퓬�I����ɔ����������Ղł��邽�ߏ��O�����B�O�i�����͉��}���狁�߂��T�Z�l�ŁA�c��R�͐�ꂩ��ב��������Ƃ���}�C�i�X�l�Ƃ����B�܂�A�R���哱���AB�R����[�P�U]�Ƃ��Ă���B
�\ 5�@��ꎟ�u���C�e���t�F���g���
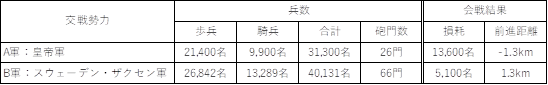
���̐킢�ɂ����ăe�B���[������c��R�͑�s���i�����B����A�O�X�^�����ɂƂ��āA���̏����͏d�v�ł��������A�A�E�X�e�����b�c���قnj���I�ł͂Ȃ������B�ȏ�̂��Ƃ���A�C���B���xMF�͍c��R��2�i�s�k�j�A�X�E�F�[�f���E�U�N�Z���R��8�i�����j�Ƃ����B
���̒n�`�͑����̋u�͂��������̂́u���n-���S�ȗ��n�v�Ƃ��A���ł���X�E�F�[�f���E�U�N�Z���R����1.05��t�^�����B�@���v�f�ɂ��ẮA�c��R�������ɂ����Ă��R���̐��ɂ����Ă���邱�Ƃ���AQJM�̋@���v�f�v�Z�����c��R��0.9��t�^�����B�Ō�ɋG�߂͎哱���ɗD�ʂȏH�̗ǍD�ȓV�C�ł��������Ƃ���A�c��R��1.1��t�^�����B
���̌��ʁA���R�̐��_�I�v�f���Ȃǂ��������P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂�A���_��͔�pB/ pA��1.68�ƂȂ��āA���͂ɂ����ėD��X�E�F�[�f���E�U�N�Z���R�������ɏ��������߂鐄�Z�ƂȂ����B�������A�A�E�X�e�����b�c���ł������ł������悤�ɁA���̐�͔�ł����Ă����ۂ̐�ʂɌ������قǂł͂Ȃ������B��ʔ�RB/RA��3.84�ł���A����ɂ��w���E�����v�f���l�����Ȃ��X�E�F�[�f���R��CEVB��2.28�ƂȂ�B
SA/SB=0.63 SB/SA=1.58
VA=1.0 �@VB=1.05
pA=SA�~VA=311,183 pB=SB�~VB=524,066
pA/pB=0.59 pB/ pA=1.68
RB/RA=3.84
CEVB=(RB/RA)/(pB/pA) =2.28
���㎮�ɂ�����A�R�͍c��R�AB�R�̓X�E�F�[�f���E�U�N�Z���R�������B
�����ŃO�X�^���̔\�͂������w���E�����v�fle��1.0�`2.0�̉ϒl�Ƃ���CEVB���v�Z�����CEV�Ȑ��́A�}1�Ɏ����Ȑ��i�}���A�m�C�W��o=1.0�j�ƂȂ�B�A�E�X�e�����b�c���ɂ�����i�|���I���Ƒ嗤�R�̕W�_�i�}���A����j����Ƃ���ƁA�O�X�^���ƃX�E�F�[�f���E�U�N�Z���R���e�B���[������c��R�ɑ��Ď������\�͂́A�قړ��ʒu�Ƀv���b�g�ł��邱�Ƃ�������B
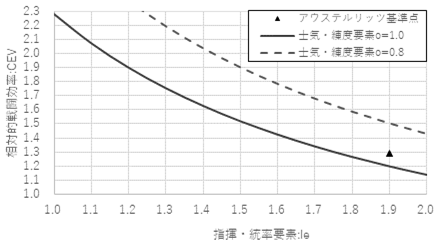
�} 1�@�w���E�����v�f��CEVB�i��ꎟ�u���C�e���t�F���g���j
�@�܂��A���̐킢�ɂ����ăU�N�Z���R�́A�C�����̃e�B���[�R�E���R�����̍U���ɑ��Ėw�ǒ�R���邱�ƂȂ��s�����Ă���A�������������ƁA�����v�Z�ɂ����ė��R����1.0�Ƃ����X�E�F�[�f���E�U�N�Z���R���̎m�C�v�fo�������ቺ�v���Ƃ���0.9�`0.8�Ƃ���]�������蓾��[�P�V]�B���̏ꍇ�ACEV�Ȑ��͐}1�̔j���Ŏ����悤�ɏ�ɐ��ڂ���B�܂�A�O�X�^���ƃe�B���[�̔\�͍����A�i�|���I���ƑΕ��哯���R��]�w�Ƃ̔\�͍��Ɠ����x�ł���Ƃ���le��1.7~2.0�͈̔͂ɂƂ�Ȃ�ACEVB��1.7�`1.1�ƂȂ�B����́A�i�|���I���̑嗤�R�ƑΕ��哯���R�Ƃ̊Ԃɂ͊�{��p�ɂ����đ傫�ȍ����Ȃ������̂ɑ��āA�e�B���[���D��K�͑��`�ƃX�E�F�[�f���R�̋@�����Ə����ȋ������d���������`�̊Ԃɂ͍��{�I�ȍ������������Ƃ��l������ƑÓ��Ȓl�ł��邾�낤[�P�W]�B
�ȏ�̂��Ƃ���AQJM�̌v�Z�ɏ]���ƁA��ꎟ�u���C�e���t�F���g���ɂ�����O�X�^���ƃX�E�F�[�f���R�̑g�ݍ��킹�́A�A�E�X�e�����b�c���ɂ�����i�|���I���Ƒ嗤�R�̑g�ݍ��킹�ɔ䌨����A���邢�͏���قnj����悭��ʂ��������ƌ��_�Â�����B
10�D��ꎟ���q��̐킢
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�3�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\6�Ɏ���[�P�X]�B�O�i�����͉��}���狁�߂��T�Z�l�ŁA�c��R�͐�ꂩ�琮�R�Ƒދp���Ă��邱�Ƃ���0.0km�Ƃ����B
���̐킢�͑S�ʉ��ł͂Ȃ����ߑ����͗��R���ɏ������B�������A�X�E�F�[�f���R���Ӑ}�����ʂ�ɓn�͂ɐ����������ŁA�c��R�͎i�ߊ�����e�B���[���d�����A���̌�Ɏ��S���Ă���B�ȏ�̂��Ƃ���C���B���xMF�́A�c��R��2�i�s�k�j�A�X�E�F�[�f���R��8�i�����j�Ƃ����B
�\ 6�@��ꎟ���q��̐킢
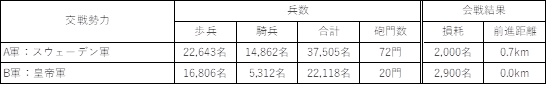
�n�`�́A���q��̑��݂ɂ��ď����v�Z�ł͍l�������A�P�Ɂu�N���n-�����n�`�v�Ƃ��Ď��i�h�䑤�j�ł���c��R�ɒn�`�v�f1.3��t�^�����B�܂��c��R�͐w�n��쉈���ɒz���ăX�E�F�[�f���R��҂��Ă������Ƃ���A�R�̑Ԑ��v�f�Ƃ��Đw�n�h�����1.6��t�^�����B����A�X�E�F�[�f���R�͎哱���i�U�����j�ł���A�������ɂ����Ă��R�����ɂ����Ă��c��R�ɗD���Ă������Ƃ���v�Z�ɂ��@���v�f1.24��t�^���A���킹�čU���ɓK�����G�߂ł��邱�Ƃ���G�ߗv�f1.1��t�^�����B
���̌��ʁA�����v�Z�ɂ�����P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂�A���_���͔�ɂ����Ă͔{�߂�����t�����Ă����X�E�F�[�f���R�ƍc��R�̍��́A1.4�{�ɂ܂ŏk�܂����B����ɂ���ʔ�RA/RB��2.83�ł��������Ƃ���A�����v�Z�ɂ�����X�E�F�[�f���R��CEVA��2.1�ƂȂ����B
SA/SB=2.06 SB/SA=0.49
VA=1.24�~1.1=1.36 �@VB=1.3�~1.6=2.08
pA=SA�~VA=493,707 pB=SB�~VB=366,186
pA/pB=1.35 pB/ pA=0.74
RA/RB=2.83
CEVA= (RA/RB)/(pA/pB)=2.1
���㎮�ɂ�����A�R�̓X�E�F�[�f���R�AB�R�͍c��R�������B
���ɂ��̑��̗v�f�ɂ��Č�������B���̐킢�ɂ����ăe�B���[�͎��R�̕����̑������V�����邢�͖����̊W�߂ł���A�w�n�����ɂ͏\���ł��邪�A���ނɂ͔\�͕s���ł��邱�Ƃ𗝉����Ă���[�Q�O]�B�����āA���R�̖ړI�������ł͂Ȃ��G�̍U����ڍ������邱�Ƃɂ����Ă����B���ہA���ʂ̋����Ƃ�����킢�ɂ����čc��R�̕����ƋR���͗ǂ�������B�ŏI�I�Ȕs�k�́A�c��R�̋R�����������ɂ����ċt�P�Ɏ��s�������Ƃɂ��B����������ł��w�n�����������͍Ō�܂ŕ���邱�Ƃ͂Ȃ������B���̎����́A�̗p������p�ɂ��V���E�����̎m�C�E���x�s���E�����Ă����ƕ]���ł���i�m�C�E���x�v�fo=1.0�Ƃ���j�B
����A�O�X�^���͂��̐킢�ł��e�B���[�������r���������B�܂��A���̓��̓n�͂̓e�B���[�̈ӕ\��˂����̂ł������B�������A�e�B���[�͒������㗤�����ɗD�镺���ł�����}�����āA�X�E�F�[�f���R�̋����Ƃ���̔@���Ȃ�O�i���j��ł���B���ǁA�X�E�F�[�f���R���ʂ̏㗤�����͏I���A��������O�i�ł��Ȃ������B����āA��P���ʂ͉͐�ɂ�����h����ʈȉ��ł���ƕ]������i��P�v�fs=1.0�Ƃ���j�B
�����œ��ɏd�v�Ȃ̂́A�e�B���[�̊�𐳖ʂ̋����Ƃ�����킢�ɓB�t���ɂ����{���ꂽ��������̉I��n�́A�����ē쑤����̑����ł���B��2,000�R�̉E���R�����͖W�Q���邱�ƂȂ���̗��ꂽ�n�_�Ń��q�쓌�݂ɓn��A�����Ƃ��U�߂�c��R�̑��ʂɐi�o�B�����ɏo���c��R�R����3,000�R�̍U�������ނ��āA���̓��̐킢�������ɓ�����[�Q�P]�B�����̎����͍c��R�����u���C�e���t�F���g�ɂ����ăO�X�^���ƃX�E�F�[�f���R�̂������w�ю���Ă����Ƃ��Ă��A�ˑR�Ƃ��ăX�E�F�[�f���R�������I�ɗD��Ă������Ƃ������Ă���iCEVA��1.0�A�O�X�^����le��1.0�j�B
�����̕]���܂��āA�}2�Ɏ������w���E�����v�f��CEVA�̊W������B���̊W�́A��ꎟ�u���C�e���t�F���g��펞�ɂ�����U�N�Z���R�̒ጸ�����l�����Ă��Ȃ��Ȑ����͂��ɉ�������B����͈ȉ��̎��������悻���藧���Ƃ������Ă���B
�i�u���C�e���t�F���g���ɂ�����U�N�Z���R�̒ጸ���j��
�i�c��R�̏K�n�x�ɂ��ጸ���j�~�i��P���ʂ�����������n�͍U���ጸ���j
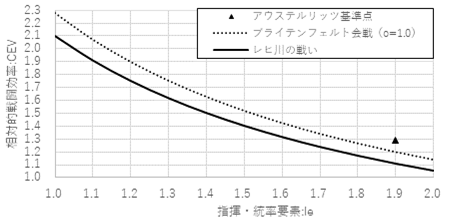
�} 2�@�w���E�����v�f��CEVA�i��ꎟ���q��̐킢�j
�܂��A���q�쓌�݂ɂ�����1.5�{�̐�͍����X�E�F�[�f���R�R�����������Ă��邱�Ƃ���ACEVA��1.5���ō��l�Ƃ������Ƃ��ł���ƕ]���ł���B�����CEVA�̍Œ�l�́A�u���C�e���t�F���g��펞�̎w���E�����v�f�̐������lle=1.9~2.0����1.1�ƂȂ�B�A���A���̍��́A�e�B���[���g���w���ʁA���������������Ȃ邱�Ƃ���ACEVA��1.5�`1.2�͈͓̔��Ɏ��܂�ƕ]���ł���B
�ȏ�̂��Ƃ���AQJM�̌v�Z�ɏ]���ƁA��ꎟ���q��̐킢�ɂ����ăX�E�F�[�f���R�́A�s���Ȑ����ɂ����āA�V��p�ɂ����ʂ�������钆�ł��A���ΓI�ɗD�ꂽ�퓬���������A�O�X�^�����e�B���[�ɗD��\�͂��������ƌ��_�Â�����B
11�D�A���g�E���F�X�e�̐킢
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�4�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\7�Ɏ���[�Q�Q]�B���R���ɑO�i�ł��Ȃ��������Ƃ���A�O�i������0.0km�Ƃ����B���̐킢�͑S�ʉ��Ɏ��邱�ƂȂ��ǒn��ŏI����Ă��܂������A�O�X�^���̃h�C�c�ɂ�����s�s�_�b��������s�k�ƂȂ����B����ŐV���ɍc��R�̎i�ߊ��ƂȂ������@�����V���^�C���́A�Ӑ}���Ă����D�ʂȏ��ł̉��ɂ܂Ŏ������ނ��Ƃ͂ł��Ȃ��������A�V�����͂̐L���������Ƃǂ߂Đ�ǂ𗧂Ē����Ƃ�����ړI��B�����邱�Ƃ��ł����B�ȏ�̂��Ƃ���C���B���xMF�́A�X�E�F�[�f���E�V���R��3�i���s�k�j�A�c��R��7�i�����I�ȏ����j�Ƃ����B
�\ 7�@�A���g�E���F�X�e�̐킢
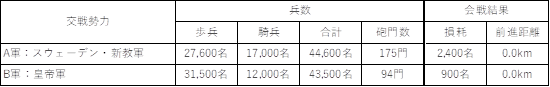
�n�`�́A�u�N���n-�����n�`�v�Ƃ��āA���i�h�䑤�j�ł���c��R�ɒn�`�v�f1.3��t�^�����B�܂��c��R�͋��͂Ȑw�n��z���ăX�E�F�[�f���R��҂��Ă������Ƃ���A�R�̑Ԑ��v�f�Ƃ��Đw�n�h�����1.6��t�^�����B
����A�X�E�F�[�f���E�V���R�͎哱���i�U�����j�ł���A�������ɂ����Ă��R�����ɂ����Ă��c��R�ɗD���Ă������Ƃ���v�Z�ɂ��@���v�f1.14��t�^���A�G�ߗv�f�Ƃ��Ă�1.1��t�^�����B�������A��x�ڂ̍U�����͓V�C�������ł��������Ƃ���A�U�����ɂ͕s���ȏƂȂ����B����ăX�E�F�[�f���E�V���R���ɒጸ���ʂƂ���0.95��t�^�����B
���̌��ʁA�����v�Z�ɂ�����P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂�A���_���͔�SA/SB�ɂ����Ă͌݊p�ŏ��s�s���̏ł��������A�n�`�Ɛw�n�̉��b�����c��R�����_��͔�pB/ pA�ɂ����ėD�����m�ۂ��錋�ʂƂȂ����B��ʔ�RB/RA��1.99�ł��������Ƃ���A�����v�Z�ɂ�����c��R�̑��ΓI�퓬����CEVB��1.24�ƂȂ����B
SA/SB=1.09 SB/SA=0.92
VA=1.14�~0.95�~1.1=1.19 �@VB=1.3�~1.6=2.08
pA=SA�~VA=244,716 pB=SB�~VB=392,427
pA/pB=0.62 pB/ pA=1.60
RB/RA=1.99
CEVB=(RB/RA)/(pB/pA) =1.24
���㎮�ɂ�����A�R�̓X�E�F�[�f���R�AB�R�͍c��R�������B
���Ɍ��ڍׂ��瑼�̗v�f�𐄎Z����B���̐킢�ɂ����ĕ�⋂ɕs���������X�E�F�[�f���E�V���R�͍c��R�̐w�n�ɑ��Đ��ʂ���U�����s�킴����A���̂܂܌��ނ��ꂽ�B�O�X�^������ɂ������͊Ԉ���Ă���A���̍��v��͊�]�I�ϑ�����Ƃ��Ă��� [�Q�R]�B
�܂����h�j�b�c����z���čc��R�w�n�̓����Ɍ����čs��ꂽ9��1���̍ŏ��̍U���́A�c��R�w�n����̖C�ɂ��j�ӂ��ꂽ�B
������9��3���ɍs��ꂽ�k���ɉ�荞��ł̓�x�ڂ̍U���́A�c��R�̐w�n�̒��ł��ł����łȏꏊ�ւ̓ːi���錋�ʂƂȂ茂�ނ���錋�ʂɏI������B���̍U���́A�c��R���ދp���ł���Ƃ���������ɂ��Ă����Ƃ������ƁA���ł��邱�Ƃ͏��m�ŁA�����ő҂��\����c��R�ƑޘH�Ɋ댯���c�����܂ܐ킢�ɋy�Ԃ����A�\�����ʉӏ��ւ̋}�P�ɂ��c��R�̐w�n�ƕ������������悤�Ƃ����̂��Ƃ����������邪�A�ǂ���ɂ���O�X�^�����G��f���ԈႦ�����Ƃɕς��͂Ȃ��B
�܂��A�X�E�F�[�f���E�V���R�͂��ĂȂ��K�͂ɖc��オ���Ă������A����ɂ�蕺⋂ɖ�������A�S�̂̋K���ቺ��O�X�^���̎w���͒ቺ�������Ă����B
����Ńe�B���[�ɑ���c��R�̎i�ߊ��ƂȂ������@�����V���^�C���͏���̍U���ɂ����Ă͐w�n���ʂ����p����͂������I�ɗp�����B��x�ڂ̌��ƂȂ���9��3���̐킢�ɂ����ẮA�w�n�̍ł��Ǝ�Ȑ����ɓG�͉�荞��ł��邾�낤�Ƒz�肵�A��͂𐼑��ɏo���ĉ��ɔ��������A�\�z�ɔ����ăX�E�F�[�f���E�V���R���w�n�k���Ɍ��ꂽ�̂�����ƁA���ꂪ�z���łȂ����Ƃ��m�F������ő����𑗂荞��œG�����ނ����B�O�X�^���̓�����ǂ��Ƃ������s��Ƃ��Ă��邪�A�w�n��a���ɂ��邱�ƂȂ������Ă������ߑ厖�ɂ͎���Ȃ������B
�ȏ�̂��Ƃ�]������ƁA���̌��ɂ�����O�X�^���ƃ��@�����V���^�C���̊Ԃ̔\�͍��̓e�B���[�قǂł͂Ȃ��A���ƕ�⋂̎�݂��X�E�F�[�f���R�̐퓬�����E�����Ɛ���ł���B�����ňȉ��̂悤�ɎO�̗v�f�ɂ��ĎZ�o�����B
�@ �w���E�����v�f�Fle=1.3
�O�X�^���ƃ��@�����V���^�C���̍��́A�O�X�^���̏������ɓ��肵�Ċw��ł����������A�����w�n�h��ł���Ȃ��玸�s�����e�B���[�Ƃ̍��قǂł͂Ȃ������Ɣ��f�ł���B�܂��A���������ɂ��t�ɃO�X�^���̎w���͂����ΓI�ɒቺ���Ă������Ƃ���������K�v������B����ă��q��̐킢�ɂ����čŏI�I�ɎZ�o���ꂽ�O�X�^����le=1.4�`1.8�����Ⴂ�l�ƂȂ�ƕ]�������B
�A ��⋁E���v�f�Fb=1/(1.5~1.2)=0.67~0.83��0.75
�X�E�F�[�f���E�V���R�̕�⋁E���̖�肪�w�n�ւ̐��ʍU���Ɍq���������Ƃ͂����炩�ł���B����āA���̗v�f�����q��̐킢�ɂ����čŏI�I�ɎZ�o�����X�E�F�[�f���R�̑��ΐ퓬����CEV=1.5�`1.2�E�����Ɣ��f���A���̋t���Ƃ����B
�B ��P�v�fs=0.9
����̍U�����ɂ����ăO�X�^���͑O������̍U�������ˌ��̌��ʂ��ߐM���āA�n�͒��ɖC�����Ĕs�k�����B�܂����ڂ̍U�����ɂ́A�c��R�̕s�ӂ�˂����Ƃ������A��ޒ��̌�q��@�����Ƃ���}���Ď��s�����B����͋t�ɃX�E�F�[�f���E�V���R���ɂƂ��Ċ�P����̂Ɠ������ʂ��������ƕ]���ł���B����ĕ����I�Ȋ�P�����Ɠ������ʂ����������ƍ��肵���B
���̎O�����������c��R��CEVB�̌v�Z���ʂ͎��̂悤�ɂȂ�B
VA=1.14�~0.95�~1.1�~0.75�~1.3�~0.9=1.04 �@VB=1.3�~1.6=2.08
CEVB=(RB/RA)/(pB/pA) =1.1
QJM�̌v�Z���ʂ́A���R���قړ����̐퓬�����Ő킢�A�c��R�����_��͔�ɑ��������ʂ����������Ƃ������Ă���B�܂�A���@�����V���^�C���́A����܂ł̐��Ŏ�����Ă����O�X�^���̐�p�\�͂ƃX�E�F�[�f���R�̎��I�D�����A��⋂��m�ۂ�����I�肷��헪��r�ƁA�w�n�h��Ƃ�����p��p���đł������A�W�߂���͂Ɍ���������������ɂ����Ƃ������Ƃ��ł���B
12�D�����b�c�F�����
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�5�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\8�Ɏ���[�Q�S]�B�c��R�̕���������̓p�b�y���n�C�����R�����̕������͏����Ă���B����͋R�����Ƃ͈قȂ�A��ꓞ�����ɂ͊��Ƀ��@�����V���^�C�����ދp�����f���Ă�������ł���B�܂��A�c��R�͒�����ۂ��đދp�������Ƃ���A�O�i�����͍c��R�Ɋւ��Ă�0.0km�Ƃ����B
�\ 8�@�����b�c�F�����
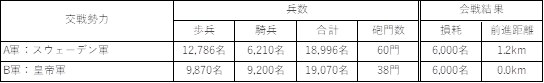
����ŔC���B���xMF�ɂ��ẮA�O�X�^���̐펀�ƍc��R�̑ދp�Ƃ�����̌�팋�ʂɂ�荸�肪������ƂȂ�B�����A���̐킢�̏��҂ɂ��Ă͌㐢�̕]������܂炸�A�X�E�F�[�f���R�̏����Ƃ���ӌ�������Έ��������Ƃ���ӌ�������B�O�X�^���̐펀���ȂāA�X�E�F�[�f���R�̐�p�I�����A�헪�I�s�k�Ƃ���l��������[�Q�T]�B�����ł܂������l�������X�E�F�[�f���R�̏����Ɣ��肵�A�X�E�F�[�f���R��MF��6�i����I�ȏ����j�A�c��R��4�i�ɔs�j�Ƃ���B�����āA���̌�A���R����5�i���������j�Ƃ����ꍇ�̍������邱�Ƃɂ��A���̍����@���Ȃ���̂ł��邩���l�@����B
�{�v�Z�ɂ����Ēn�`�́A�u���n-�����n�`�v�Ƃ��āA���i�h�䑤�j�ł���c��R�ɒn�`�v�f1.2��t�^�����B�܂��c��R�̓X�E�F�[�f���R�̍U���ɑ��āA���Ԃ̋u��ȈՓI�Ț͍��Ȃǂ̖h��Ԑ����ȂĂ�����}�����������Ƃ���A�R�̑Ԑ��v�f�Ƃ��ĉ��}�h�����1.3��t�^�����B����A�哱���i�U�����j�̃X�E�F�[�f���R�ɂ��ẮA���̏o�Ă����C��v�f���������ċC��v�f0.9��t�^����Ƌ��ɁA�������ɂ����Ă��R�����ɂ����Ă�����Ă������Ƃ���v�Z�ɂ��@���v�f0.95��t�^�����B
���̌��ʁA�����v�Z�ɂ�����P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂�A���_���͔�SA/SB�ɂ����Ă̓X�E�F�[�f���R�D���̌��ʂƂȂ�Ȃ���A�n�`�Ɛw�n�A�C��̉��b�����c��R�����_��͔�pB/ pA�ɂ����ėD�����m�ۂ��錋�ʂƂȂ���[�Q�U]�B���������ʂ́A������B
SA/SB=1.24 SB/SA=0.80
VA=0.95�~0.9=0.86 �@VB=1.2�~1.3=1.56
pA=SA�~VA=121,881 pB=SB�~VB=178,144
pA/pB=0.68 pB/ pA=1.46
RA/RB=1.88�iMFA=6, MFA=4�̏ꍇ�j
CEVA= (RA/RB)/(pA/pB)=2.75
���㎮�ɂ�����A�R�̓X�E�F�[�f���R�AB�R�͍c��R�������B
�����ōŏ��ɁA�O�X�^������уx�����n���g�̎w���E�����v�fle�ɂ��ĕ]�����s���B�A���g�E���F�X�e�ł̓O�X�^���ƃ��@�����V���^�C���̍��Ƃ��āAle=1.3�ƒu�����B�������A����ŃA���g�E���F�X�e�͐w�n�h���ł���A���ɂ�����S�ʉ��ł͂Ȃ������B�����ă����b�c�F���ɂ����ă��@�����V���^�C���̓p�b�y���n�C���R�������Ă��܂�����ԂŌ����J�n���˂Ȃ�Ȃ��Ƃ������f�~�X�����Ă���B
����ŃX�E�F�[�f����������ƁA���r���ŃO�X�^���͐펀���A�S�̎w���̓x�����n���g�ɔC����Ă���B�������x�����n���g�́A���̐킢�Ō����ɑS�R�̎w���������A�����̗���������Ȃ������B�l���g�����Q���ɂ����Ĕs�k���Ă͂�����̂́A�ނ�����ꗬ�̌R�l�ł��������Ƃ́A���̌�̐��������ؖ�����Ă���B
�����̎����ƁA��ꎟ�u���C�e���t�F���g���ɂ�����O�X�^���ƃe�B���[�̍����l������ƁA�X�E�F�[�f���R��]�w�ƃ��@�����V���^�C���̔\�͍��̓A���g�E���F�X�e�������傫���ƕ]���ł��邽�߁Ale=1.4�`1.7�Ɛ��Z�ł���[�Q�V]�B
���̐��l��O��Ƃ��āA�X�E�F�[�f���R������I�ȏ��������߂��ƕ]������ꍇ�ɂ��čl�@����B���̏ꍇ�A��ʔ�RA/RB��1.88�ƂȂ�A�X�E�F�[�f���R�̎b��I��CEVA��1.92�`1.62�ƂȂ�B
RA/RB=1.88
VA=0.95�~0.9�~1.4�`1.7=1.26�`1.53 �@VB=1.2�~1.3=1.56
CEVA= (RA/RB)/(pA/pB)=1.92�`1.62
����A���q��̐킢�ɂ����čŏI�I�ɎZ�o���ꂽ�c��R�̃X�E�F�[�f���RCEV��1.2�`1.5�ł��邱�Ƃ���A��ʓI�ȃX�E�F�[�f���RCEVA��1.3�ƒu�����Ƃ��ł���B�܂�A�b��I��CEVA�ƁA���т��狁�܂�CEVA�̊Ԃɂ�1.52�`1.25�̍����������B
������ǂ̂悤�ɐ�������Ηǂ����낤���H�@��̐����Ƃ��āA�ȉ��̌v�Z���ʂ������B����͌v�Z�l�Ǝ��ђl�̍����A�O�X�^���̐펀/�����̏��ɂ��X�E�F�[�f���R�̐퓬�ӗ~�����サ�����ʂł��������Ƃ��������̂ł���B
�N���E�[���B�b�c�͐푈�ɂ����Đ��_�I�v�f�����Ă͂Ȃ�Ȃ��Ƃ���B�����āA���̐킢�ɂ����ăX�E�F�[�f���R�����͖��炩�ɒʏ�Ƃ͈قȂ鐸�_��Ԃɂ������B�������O�X�^���펀�̕ǂ�قǃX�E�F�[�f���R���m�����ɒm��n���Ă����̂��ɂ��Ă͗l�X�Ȉӌ�������[�Q�W]�B�������A�㋉�w���������͊ԈႢ�Ȃ������펀�̏���͂�ł������A���m�����ɂ����Ă��O�X�^�������Ȃ��Ƃ��d�����Đ�ꂩ��p�����������ƁA�����Ďw���������̏�Ȃ�ʈӗ~�ɋC���������Ƃ��낤�B��u�̃p�j�b�N�̌�A�ނ�͊F�A������ނ̌��ӂ������A���̂悤�Ȍ��ӂ͌R�����_�̔��I�ɑ傫���e�����y�ڂ����Ɛ��肳���B
�����ŁA�c��R�̃X�E�F�[�f���RCEVA�����ђl1.3�ƂȂ�悤�Ɏm�C�E���x�v�fo���߂�ƃX�E�F�[�f���R�̐��v�f�W���͕\9�̂悤�ɂȂ�B
�\ 9�@�����b�c�F�����ɂ�����X�E�F�[�f���R�̐��v�f�W���iMFA =6�j
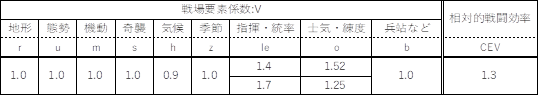
����܂�����ŁA���ɂ��̌�킪���������ł������ƕ]������ꍇ�ɂ��čl�@����B����́A�O�X�^���펀�̉e�����X�E�F�[�f���R��MFA��6����5�Ɉ��������A�t�ɍc��R��MFB��4����5�Ɉ����グ���ƌ��Ȃ��l���ł���B���̏ꍇ�A��ʔ�RA/RB��1.48�ƂȂ�B���̂Ƃ��A�X�E�F�[�f���R��]�w��le��1.4�`1.7�ACEVA�����ђl1.3�Ƃ���ƁA�X�E�F�[�f���R�̐��v�f�W���͕\10�̂悤�ɂȂ�B
���ʂ�����ƁAMF�𗼌R����5�Ƃ������ʁA�m�C���g���ʂ�1.0�ɋ߂Â����Ƃ�������Ă���B�܂����Ɏw���E�����v�f���傫���A�܂�O�X�^���̉��l�������ق�1.0�ɋߎ�����Ƃ�������B
�\ 10�@�����b�c�F�����ɂ�����X�E�F�[�f���R�̐��v�f�W���iMFB =5�j
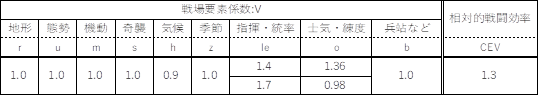
����̓O�X�^���펀�ɂ�鑹�������iMFA =6�j�A�����т���X�E�F�[�f���RCEVA=1.3���K��l�Ƃ���ƁA�펀�ɋN������m�C���g���ʂ�1.5�`1.3�ƂȂ邪�A�펀�ɂ�鑹�����܂�Ő�ʔ���Čv�Z����ƁiMFA =5�j�A�m�C���g���ʂ̑啔���͐펀�����ɂ���đ��E����Ă��܂��Ƃ������Ƃ������Ă���B
�ȏ�̂��Ƃ���AQJM�͏����̐�Ӎ��g��������x�͈̔͂Œ�ʉ����邱�Ƃɐ������Ă���A���̌��ʁA�����i�펀�j�ƌ��ʁi�m�C���g�j�̈��ʊW�͓����ŕ\�������B����́A�����b�c�F�����ɂ����鏟�s���������ӌ��̑���ɑ��āA��̎����������̂ł��낤�B
�i�펀�ɂ��C���B���x�̒ቺ�j���i�m�C���g�ɂ����m�ہj
13�D�l���g�����Q�����
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�6�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\11�Ɏ���[�Q�X]�B���̐킢�ɂ����ĐV���R�i�n�C���u���������R�j�Ƌ��ɐ�����X�E�F�[�f���R�͉�œI�ȑ��Q����A��̎��オ�I��������Ƃ����炩�ƂȂ����B���������c��͋�������ѐV���̑����̒鍑����ƊԂŃv���n������茋�сA�푈�̈ꎞ�I�������l�������B�ȏ�̂��Ƃ���C���B���xMF�́A�X�E�F�[�f���E�V���R��2�i�s�k�j�A�c��R��8�i�����j�Ƃ����B�܂��A��ꂩ��ב������X�E�F�[�f���E�V���R�̑O�i�����̓}�C�i�X�l�Ƃ����B
�\ 11�@�l���g�����Q�����
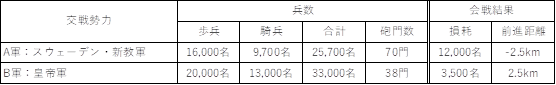
�n�`�́A�u�N���n-�����n�`�v�Ƃ��āA���i�h�䑤�j�ł���c��R�ɒn�`�v�f1.3��t�^�����B�܂��c��R�̓X�E�F�[�f���E�V���R�̍U���ɑ��āA�\���Ȗh��Ԑ����ȂĂ�����}�����������Ƃ���A�R�̑Ԑ��v�f�Ƃ��Ėh�����1.5��t�^�����B����A�哱���i�U�����j�̃X�E�F�[�f���E�V���R�ɂ��ẮA�C���̗D�z���������R�����p�ł���n�̐����͂��ɑ����v�Z�ƂȂ邽�߁A�@���v�f�Ƃ���1.05��t�^�����B�܂��R�̋@���ɓK�����G�߂ł��邽�߁A�U�����ł���X�E�F�[�f���E�V���R�ɋG�ߗv�f1.1��t�^�����B
���̌��ʁA�����v�Z�ɂ�����P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂����B���_���͔�SA/SB�ɂ����ċ͂��ɗ̌��ʂƂȂ����X�E�F�[�f���E�V���R�́A�lj��v�f�Ƃ��Ď��ɈՂ��n�`�̌��ʂƍU����\�����������ɂ��c��R�̐�͂��{�����ꂽ���Ƃɂ��A���_��͔�pB/pA�ɂ����č����L�����A���|�I�Ȕs���̗���ɒǂ����ꂽ�B�������X�E�F�[�f���E�V���R����������ۂ̑��Q�́A�X�ɂ��̔{�ł������B
SA/SB=0.85 SB/SA=1.18
VA=1.05�~1.1=1.15 �@VB=1.3�~1.5=1.95
pA=SA�~VA=160,500 pB=SB�~VB=319,924
pA/pB=0.5 pB/ pA=1.99
RB/RA=4.0
CEVB=(RB/RA)/(pB/pA) =2.01
���㎮�ɂ�����A�R�̓X�E�F�[�f���E�V���R�AB�R�͍c��R�������B
����܂ł̌v�Z���ʂ������Ă����ʂ�A�����������X�E�F�[�f���R�͐������ւ�A�V�@���̐�p���ʂ����܂��āA�c��R��ŏ��CEV=1.3���x�̌��������Ă����B�����ăO�X�^����M���Ƃ����D�G�Ȏ�]�w�́A�⊶�Ȃ����̎w���͂Ɠ����́A��p�I��r�����������߁A�����̏ꍇ�Ő�͔�ȏ�A�Ȃ����͐�͔�ʂ�̌��ʂ���ɂ��Ă����B�������A���̐킢�ɂ����āA�����̌��ʂ͖w�nj����Ȃ��B�ނ�̐킢�U��͐ٗ�ł���A��]�w�ɋ������͌����Ȃ������B
���ɁA���̌��ɂ����ăX�E�F�[�f���R�i�ߊ��z�����ƐV���R�i�ߊ��x�����n���g���A�݂��ɋ��͂������Ȃ��������Ƃ͒��ڂɒl����B�Ë��ĂɊ�Â��Ĕނ�̓o���o���ɐ킢�A�����Ė��d�ȍU���Ɏ��s���A���삷��ׂ��Ƃ�������삹���ɔs�ꋎ�����B����A�c��R�̎�]�w�͋����𗝉����Ă����B�X�E�F�[�f���E�V���R�����́u�ň��̎���v���������Ƃ���Ȃ�A�c��̒��j�n���K���[���t�F���f�B�i���g����уX�y�C�����̖���t�F���i���h���@���̓�l�̎w�����Ɠ�̃n�v�X�u���N�R�́A���́u�ŗǂ̎���v�����̐킢�Ŏ����� [�R�O]�B
�܂�A���̐킢�ʼne���̑傫�����v�f�W�����X�ɋ��߂�Ƃ���Ȃ�A����͗��R�̎w���E�����v�fs�ɂ�����Ⴂ�ƂȂ�B�X�E�F�[�f���E�V���R���̎w���E�����v�f�́A��l�̎w���������ꂼ��܂�ňႤ�킢�����Ă��邩�̂悤�ł��������Ƃ���A��v���Č��ɑΏ������c��R�Ɣ�r����ƁA���傤�ǔ����ɂȂ邱�Ƃ��P���ɐ����ł���B������sA=0.5�Ƃ���Ȃ�Η��R��CEV��1.0�ƂȂ�B
����͗��R����͔�ʂ�ɐ�ʂ����������Ƃ������Ă���A���ꂼ��̐���ɂ����Ă͑P�킵���X�E�F�[�f���E�V���R�ɂ��Ă��A�ނ�ɗ��ʐ킢�U��ŏ�������ɂ����c��R�ɂ��Ă��A�������K�ɕ]���ł��Ă���Ɣ��f����B
���̌v�Z���ʂ������Ă��邱�Ƃ́A�܂������}�L�����F�b�����q�ׂĂ���ʂ�A�u��R�̎w�����́A��l�ł���ׂ��ł���B�i�����j��l�̗D�ꂽ�l����h����������A��l�̖}�l��h�������ق����A�͂邩�ɗL�v�ł���v[�R�P]�Ƃ����w�E�̐������ł���A���̓_�Ɋւ��A�c��R����������Ƃ��Ă��邪�A�݂��ɒ��荇�����ƂȂ��u��l�̖}�l�v���݂̗͂������Ƃ����邾�낤[�R�Q]�B
14�D���B�b�g�X�g�b�N���
QJM�̊�{�v�Z�l�ƌ��ʂ�ʎ�7�Ɏ����B�܂��O��ƂȂ闼�R�����Ƒ��Ղɂ��ĕ\12�Ɏ���[�R�R]�B���̐킢�͌����đ�K�͂ȉ��ł͂Ȃ��������A�h�C�c�ɂ����Ēn�������������Ă����X�E�F�[�f���ɂƂ��āA���M�����߂����|���ƂȂ�킢�ł���A�O�\�N�푈�㔼���Ɏ����̓]���_�ƂȂ����B
�X�E�F�[�f���R�̑O�i�����͉��n�}����5.0km�Ɛݒ肵�A�s�k�����c��R�͐h�����ē����^�钆�܂ł͐��ɗ��܂��Ă������Ƃ���0.0km�Ƃ����B�܂��A�X�E�F�[�f���R�ɂƂ��Ė{���̏����͋N���̏o�����ł���A�c��R�ɂƂ��Ă̓l���g�����Q���ȍ~�̗D�ʂ����S�Ɏ����_�@�ƂȂ�s�k�ł�����[�R�S]�B�ȏ�̂��Ƃ���C���B���xMF�́A�X�E�F�[�f���R��8�i�����j�A�c��R��2�i�s�k�j�Ƃ����B
�\ 12�@���B�b�g�X�g�b�N���
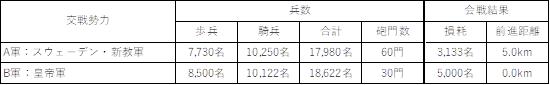
�n�`�́A�u�N���n-�����n�`�v�Ƃ��āA���i�h�䑤�j�ł���c��R�ɒn�`�v�f1.3��t�^�����B�܂��c��R�͋u�̏�Ś͍����@��A�הn�Ԃ�A�˂Ėh��Ԑ��𐮂��Ă������Ƃ��牞�}�h�����1.3��t�^����[�R�T]�B����A�哱���i�U�����j�̃X�E�F�[�f���R�ɂ��ẮA�R���ƖC���̗D�z�������@���͂���ł���Ƃ��āA�v�Z����@���v�f1.07��t�^�����B�܂��R�̋@���ɓK�����G�߂ł��邽�߁A�U�����ł���X�E�F�[�f���R�ɋG�ߗv�f1.1��t�^�����B
���̌��ʁA�����v�Z�ɂ�����P���Ȑ��v�f�W��V�͈ȉ��̂悤�ɋ��܂����B���_���͔�SA/SB�ɂ����ď��s�s���ƂȂ鍷�́A�L���Ȓn���Ɩh����ʂ����܂��ė��_��͔�pB/pA�ɂ����Ă͍c��R�ɌR�z���オ���͍��ƂȂ����B
���������ʂ͐^�t�ƂȂ�B��ʔ�RA/RB��3.24�ł���A�����v�Z�ɂ�����X�E�F�[�f���R��CEVA��4.35�ƂȂ����B
SA/SB=1.07 SB/SA=0.93
VA=1.07�~1.1=1.17 �@VB=1.3�~1.3=1.69
pA=SA�~VA=67,061 pB=SB�~VB=90,126
pA/pB=0.74 pB/ pA=1.34
RA/RB=3.24
CEVA= (RA/RB)/(pA/pB)=4.35
���㎮�ɂ�����A�R�̓X�E�F�[�f���E�V���R�AB�R�͍c��R�������B
����͋ɂ߂č����퓬�����ł���A���ɉ��炩�̐��v�f�W��������̂ł͂Ȃ����Ɛ��������B�����������̃X�E�F�[�f���R�́A�ˑR�Ƃ��čc��R�ɔ�ׂĂ̎��̍�����]������Ă͂������̂́A�O�X�^�������̐������������Ă����B
����ő���Ɏw���E�����v�f�ɖڂ������邱�Ƃ͂ł���B�Ⴆ�X�E�F�[�f���R�w�����ł���o�l���A�����Ă��̔z���ɂ��������Y���[�A�g���X�e���\���A�L���O��́A�ԈႢ�Ȃ��c��R�̎w�����n�b�c�t�F���g�������\�͓I�ɗD��Ă����B�������A�ނ�X�E�F�[�f���R��]�w�̎w���E�����v�f���A�i�|���I�����݂̒l�ile=1.9�j�Ƃ��Ă�CEV A��2.18�ƂȂ�A��ꎟ�u���C�e���t�F���g��퓖���̐����ȃX�E�F�[�f���R�̍ő各��l1.7�������Ă��܂��B�������A�X�E�F�[�f���R�̎�]�w�́A���i����e�c���̋����ɖw�ǎ��s���Ă���A�\���c�����w�������t�B�b�c�g�D���́A�o�l���ւ̔�������Ӑ}�I�ɑO���ւ̐i�o��x�点�A��͕�������@�Ɋׂꂽ�Ƃ����Ă���[�R�U]�B�ȏ�̂��Ƃ��瑊�Βl�ł������Ƃ��Ă��Ale��1.9�܂ō��߂邱�Ƃ͉ߑ�]���ƂȂ�Ɣ��f����B�ł́A���ɂǂ̗l�Ȑ��������藧�̂ł��낤���H
�����Œ��ڂ���ׂ��Ȃ̂͌R�̑Ԑ��i���`�ԁj�ł���B����܂ōU�����ɑ��Ă��̒l�͏��1.0�ł������B���������ʍU������̓˔j���邢�͑��ʍU���A�Ȃ����͐w�n�h��Ȃǂł���������܂ł̎���Ƃ͈قȂ�A���̉��ɂ����ăo�l���͑�_�Ȑ�p�I���i�����ɂ���͋@���ŋ����i������́j�ɐ�������[�R�V]�B������́i���S��́j�𐬂��������Ñ�̃J���l�[���Ɏ��܂łł��Ȃ��A��͂��ł��퓬���������܂���`�Ԃł��邱�Ƃ͐�j���ؖ�����Ƃ���ł���[�R�W]�B�������A�o�l������}�����R�����Ă̋@���͑傢�Ȃ�q���ł���A�n�b�c�t�F���g���L�\�ł���A���炭�X�E�F�[�f���R�̕�͋@���͎��s���A�e���j����Ă����ł��낤�B�������A�o�l���͓q���ɏ������B���̔z���͔���ł������B
�ߐ����[���b�p�̐��ɂ������͌��ʂ��A�{���̈�Ⴞ���Œ�ʉ����邱�Ƃ͂ł��Ȃ��B�������A����̌v�Z�̒�ʉ����I�͂���Ȃ��̂łȂ��Ƃ���Ȃ�A���Ȃ��Ƃ���͂ɐ��������ꍇ�A��͂�{��������ʂ����������ƕ]���ł��邾�낤�B
15�D���_
�{�e�ɂ����Čv�Z�������ʂ�\13�Ɛ}3�Ɏ����B�w���E�����v�f��m�C�E���x�v�f���l�����Ȃ��ꍇ�ɂ����Ă��A��ꎟ�l���g�����Q���ɂ�����s��������āA�X�E�F�[�f���R�̍c��R��Ƃ����Ƃ��̑��ΓI�퓬�����́A1�ɋߎ����邩�A1�ȏ�ƂȂ��Ă���B�܂��}3�̑�l�ی��ɕW�_���Ȃ����Ƃ́A��͗̂Ƃ��A�c��R���퓬�����ɂ���Đ�͍������Ƃ��ł��Ȃ��������Ƃ������Ă���B�t�ɑ��ی��̕W�_�������ʂ�A�X�E�F�[�f���R�͓�̎���ɂ����Đ�͍���퓬�����ɂ�蕢�����B
�����̌��ʂ�l�X�Ȏ�������Ĉ�ʉ��̂��߂ɕ��ς��Ƃ�ƁA�w�����̔\�͂�_�I�v�f�����������ꍇ�A�X�E�F�[�f���R�̑��ΓI�퓬�����͑c��R���2�{�A�R�̐������݂̂��l�����ꍇ�A�c��R���1.5�`1.3�{�ƂȂ�B
�ȏオQJM�̎�@�Ɋ�Â��v�Z���ꂽ�A��j���q�ׂ�Ƃ���̃O�X�^���̍˔\�ƃX�E�F�[�f���R�̐�������������ʒl�ł���B
�\ 13�@�X�E�F�[�f���R�̗��_��͔�Ɛ�ʔ�A����ё��ΐ퓬����
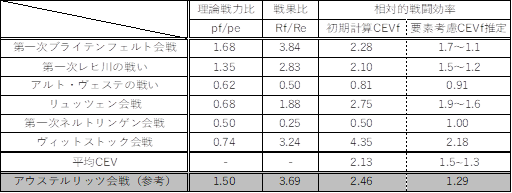
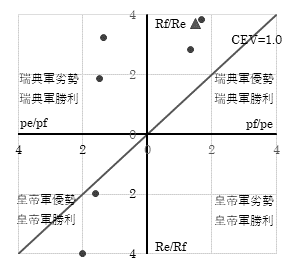
�} 3�@���_��͔�Ɛ�ʔ��i���F�A�E�X�e�����b�c�Q�l�_�j
�ӎ��F
�{�e���쐬����ɂ�����A��ʉ����胂�f���������Ē����܂����u���S�ۏ�w���w�ԁv��ÎҁA�����a�l�l�i@Kazuto_Takeuchi�j�Ɋ��ӂ̈ӂ�\���܂��B
�{�e�ŗp����ꂽQJM��Η͕]�_���f���A�܂��A���̑��̗l�X�Ȑ����A�R���Ɋւ��鎖���ɂ��Ă̏Љ�͈ȉ��́A�����^�c����Ă���u���O�L���ɂēǂނ��Ƃ��ł��܂��B
�@�w�p�u���O�u���S�ۏ�w���w�ԁv�ihttps://militarywardiplomacy.blogspot.jp�j
[�P] ���{��̏��Ђɂ����Ă͈ȉ����Q�Ƃ��邱�ƁB���`���[�h�E�u���W���X�L�[�A���я��q��w�O�X�^���E�A�h���t�̋R���x�i�V�I���ЁA2001�N�j; ���`���[�h�E�u���W���X�L�[�A���я��q��w�O�X�^���E�A�h���t�̕����x�i�V�I���ЁA2001�N�j; �I�I�^�A����u18���I�����܂ł̋R����p�̕ϗe�v�w�ߐ��ߑ�R���������x�T�[�N���R�����i�Ђ������j�ҁi���l���A2017�N�j�B
[�Q] T. N. Dupuy, Numbers, Predictions and Wars, Revised Ed (Fairfax: Hero Books, 1985); T. N. Dupuy, Understanding War: History and Theory of Combat (New York: Paragon House Publishers, 1987).; �ѓc�k�i�w�퓬�̉Ȋw�@���� �R��OR�̗��_�x�i�O�b�ЁA2010�N�j392–408�B���Ɂw�����@�R��OR�̗��_�x�͓��{��ł̊T�v���L�ڂ���Ă��邽�ߗ����̂��߈�ǂ𐄏�����B�܂��A���_�̏ڍׂɂ��ẮA�f���s���C�̌������Q�Ƃ��邱�ƁB
[�R] �ȉ��ɂ����Ďg���Ă���e���q�̐����⓱�o�̏ڍא����͕ʍe��p�ӂ���\��ł���A�{�e�ł͏ȗ������B
[�S] Dupuy, Numbers, Predictions and Wars, 26. �f���s���C�́u������v�u�R�����v�u�R���p�s�X�g���v�u12�|���h�C�i17C�j�v�ɂ��Ē����ŎZ�o���Ă���A����ȊO��TLI�͕���̔\�͂ƃf���s���C�̒l���r�����o�����B
[�T] Ibid., 28–29; Dupuy, Understanding War: History and Theory of Combat, 84.
[�U] �Ȍ�ŗ��p����e�W���̊�{�l�͈ȉ����Q�Ƃ��邱�ƁBDupuy, Numbers, Predictions and Wars, 228–31.
[�V] Dupuy, Understanding War: History and Theory of Combat, 67.
[�W] Dupuy, Numbers, Predictions and Wars, 104–5.
[�X] �{�e�ɂ����Ă͂��ꂼ��̐킢�̏ڍׂɂ��Ă͋L�q���Ȃ��B�ڍׂ�m�肽���ꍇ�͊e���Ђ��Q�Ƃ��邱�ƁB
[�P�O] Ibid., 151–54; Dupuy, Understanding War: History and Theory of Combat, 267–69.
[�P�P] �@���v�f�͌v�Z�ɂ��Z�o�����B�ȉ����Q�Ƃ̂��ƁBDupuy, Numbers, Predictions and Wars, 36.
[�P�Q] ��ʔ�̎���WW.II�̎��т�����R�Ɨ��_��͔�p/p����Z�o���ꂽ��ʐ퓬�ߎ����ł���B�ȉ����Q�Ƃ̂��ƁBIbid., 60–61.�@�Ȃ���ʐ퓬�Ƃ�CEV=1�ƂȂ�퓬�������B
[�P�R] �i�|���I�����g�͎���̉��l���\���̕��ɓ������Əq�ׂĂ���BDigby George. Smith, The Decline and Fall of Napoleon�fs Empire : How the Emperor Self-Destructed (London: Greenhill Books, 2005), 231.
[�P�S] �Ȃ��A���f���̐��m������ׂ������l�̑召�͈Ӗ��̂Ȃ����̂Ɣ��f���Ă���B
[�P�T] William P. Guthrie, Battles of the Thirty Years War: From White Mountain to Nordlingen, 1618-1635. (London: Greenwood Press, 2002), 20–23, 35–37.
[�P�U] �ȍ~�A�S�Ă̍l�@�ɂē��l�Ƃ���B
[�P�V] �Ⴆ��1982�N�̃��o�m���푈�ɂ����āA6��10���ȍ~�̃V���A�R�̎m�C�]���Ƃ���0.9���f���s���C�͗p���Ă���BDupuy, Understanding War: History and Theory of Combat, 248.
[�P�W] �u���C�e���t�F���g�ɂ����ăe�B���[����K�͂ȃX�y�C�����w�i�������ʂɌ�����Ƃ���̃e���V�I���`�j��p���Ă������ɂ��Ă͈٘_������B�������X�y�C�����w�łȂ��Ƃ��A�e�B���[����K�͂ȕ������`���D���Ƃɋ^���͂Ȃ��B�Ⴆ�X�E�F�[�f���R�̕��i�ߊ��z�������R�̃u���C�e���t�F���g�ɂ�����L錄�ł́u4�̋���ȃX�y�C������`�i16�A���ō\���j���E���ɂ������R�������āv�ƕ\������Ă���B�u���W���X�L�[�w�O�X�^���E�A�h���t�̋R���x36�ŁGLaurence Spring, The Bavarian Army during the Thirty Years War, 1618-1648 : The Backbone of the Catholic League (West Midlands: Helion and Company, 2017), 105; Guthrie, Battles of the Thirty Years War: From White Mountain to Nordlingen, 1618-1635., 10.
[�P�X] Ibid., 181–82.
[�Q�O] Ibid., 167.
[�Q�P] Ibid., 168.
[�Q�Q] Ibid., 203–7, 220–23.
[�Q�R] Ibid., 189–93.
[�Q�S] Ibid., 223–26.
[�Q�T] Ibid., 218–19.
[�Q�U] �v�Z��A�p�b�y���n�C���̋R����͂��܂߂Ă��邪�A���ۂ͓r������̎Q���ƂȂ邽�߁A���̍��͂��������k�܂邾�낤�B
[�Q�V] �A���茵�����ӌ����ׂ̂�Ȃ�A���̉��ɂ����ă��@�����V���^�C�����O�X�^�����x�����n���g���A�����Ɏ�Ђǂ��~�X�����Ă���B���@�����V���^�C���͉��v��ɂ����ĎI�ɉ߂������A�O�X�^���̖��̒��ł̍��w���͖��d�������B�x�����n���g�ɂ����Ă���풆�Ղ܂ł̖��d�ȍU���ɂ���͂�Q��Ă���BIbid., 217. �������A�{�e�ɂ����邠����W���͑��Βl�ł��邱�Ƃ�Y��Ă͂Ȃ�Ȃ��B
[�Q�W] Ibid., 215.
[�Q�X] Ibid., 265–68, 284–89.
[�R�O] Ibid., 275.
[�R�P] ���쎵���w�}�L�A�x�b����^�x�i�V���ЁA1992�N�j123–24�ŁB
[�R�Q] �����Ƃ��A�}�[���o�����ƃI�C�Q�����̂悤�ȑ�z������l�̎w�����ɂ���z���������Ƃ�����������݂���B���͋�������ӎ��Ƃ��̒i�K�ɂ���̂��낤�B
[�R�R] William P. Guthrie, The Later Thirty Years War: From the Battle of Wittstock to the Treaty of Westphalia (London: Greenwood Press, 2003), 48–51, 61–68.
[�R�S] �����Ƃ��A���̐킢�ɎQ�����������e�N�b�R���͌���I�Ȑ킢�ł͂Ȃ������ƒ�`���Ă���AMF��7�F3���x�ɂ��Ă��ǂ���������Ȃ��BIbid., 57.
[�R�T] �������c��R�̐w�n�͖k�����ʂ݂̂ł���A�n�b�c�t�F���g�������̖h���a���ɂ������Ƃ͒v���I�Ȍ��ł������B
[�R�U] Ibid., 56–57.
[�R�V] ���̉��ɂ����ăo�l���͗\�����܂߂�4�c���ŗ�����͂�_�����Ƃ����Ă���BIbid., 52.
[�R�W] �ߐ����[���b�p�̖��ɂ������͂̐��͗]�葽���Ȃ����A�Ⴆ�Η����˔j����̗�����͂ɐ��������t���E�V���^�b�g�̐킢�ł́A�X�E�F�[�f���R�����悻2�{�̓G��r�ł��Ă���B